[stl 源码分析] std::sort

std::sort 是标准库里比较经典的算法，它是一个复合排序，结合了几种算法的优点。

1. 概述
- 1.1. 算法优缺点
- 1.2. 算法结合
2. 源码
3. 小结
4. 参考

1. 概述

std::sort 主要是三种算法的结合体：插入排序，快速排序，堆排序。

1.1. 算法优缺点

算法	时间复杂度	优点	缺点
插入排序	O(N*N)	当数据量很少时，效率比较高。	当数据量比较大时，时间复杂度比较高。
快速排序	平均 O(NlogN)，最坏 O(NN)	大部分时候性能比较好。	算法时间复杂度不稳定，数据量大时递归深度很大，影响程序工作效率。
堆排序	O(N*logN)	算法时间复杂度稳定，比较小，适合数据量比较大的排序。	堆排序在建堆和调整堆的过程中会产生比较大的开销，数据量少的时候不适用。

1.2. 算法结合

std::sort 根据上文提到的几种算法的优缺点，对排序算法进行整合。

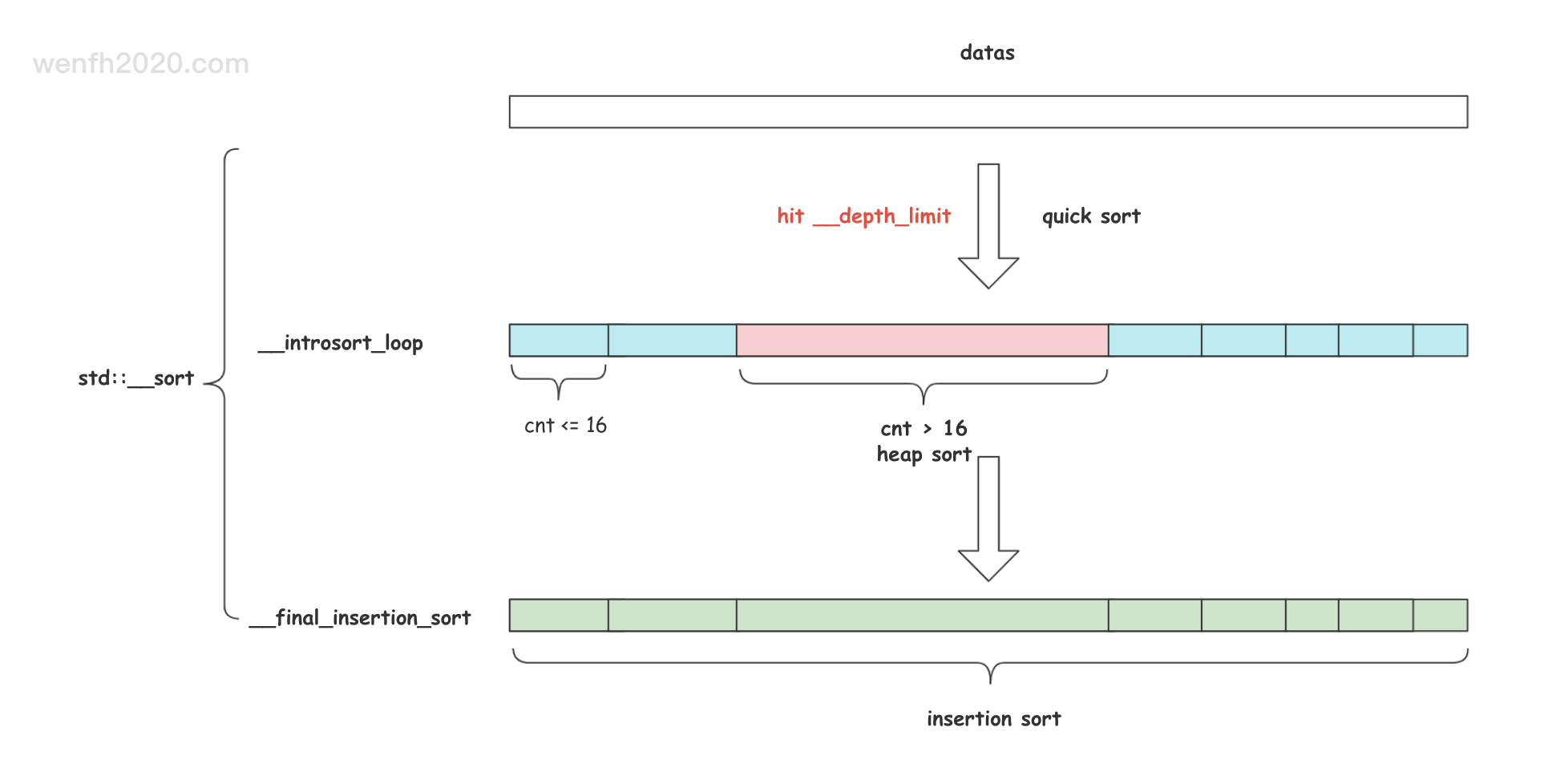
快速排序，递归排序到一定深度后，数据已经被分为多个子区域，子区域里面的数据可能是无序的，但是子区域之间已经是有序了。
在这多个子区域里，如果某个子区域数据个数大于阈值（16），采用堆排序，使得某个子区域内部有序。
剩下的没有被堆排序的小区域，数据量都是小于阈值的，最后整个数据区域采用插入排序。

这种被优化的快速排序+堆排序，被称为 内省排序（introspective sort）。

2. 源码

2.1. 测试

/* g++ -g -O0 -W -std=c++11 main.cpp -o test && ./test */
#include <time.h>

#include <algorithm>
#include <iostream>
#include <vector>

#define MAX_LEN 1000000
#define LIMT_CNT 100

int main() {
    int limit = 0;
    std::vector<int> nums;
    nums.reserve(MAX_LEN);

    srand((unsigned)time(NULL));

    for (int i = 0; i < MAX_LEN; i++) {
        nums.push_back(rand());
    }

    std::sort(nums.begin(), nums.end(), std::less<int>());

    for (auto v : nums) {
        std::cout << v << " " << std::endl;
        if (++limit > LIMT_CNT) {
            break;
        }
    }
    return 0;
}

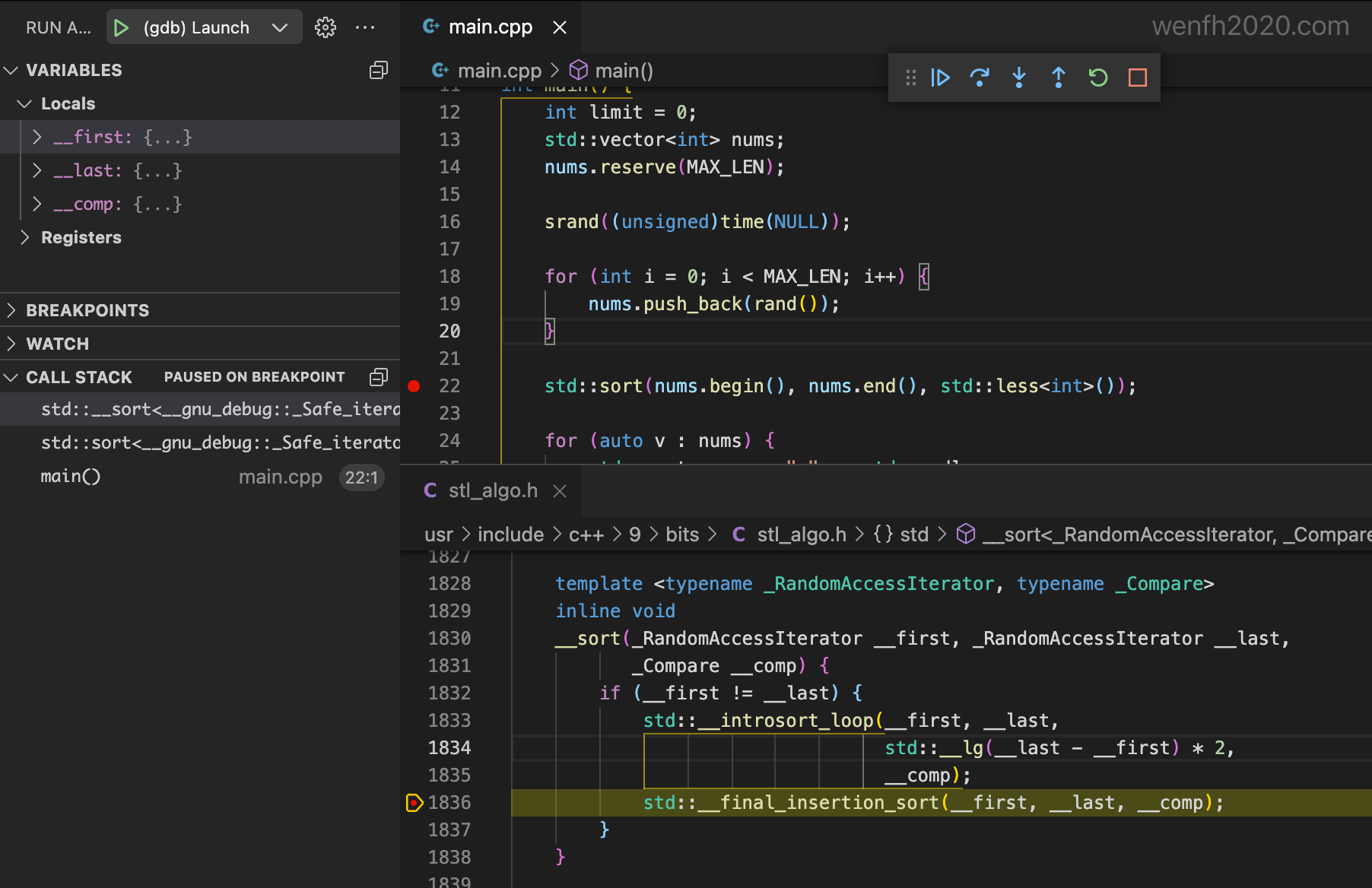
2.2. 调试

动手调试源码，逻辑会更清晰 😁。（ubuntu 调试环境搭建）

2.3. stl 源码分析

2.3.1. 函数调用关系

std::sort
|-- std::__sort
    |-- __introsort_loop
        |-- __unguarded_partition_pivot # 将某个区域的数据根据哨兵分离出两个子区域，并返回这两个子区域的分界位置 __cut。
        |-- __introsort_loop # 递归。
        |-- __partial_sort -- if (__depth_limit == 0) # 快排到达指定深度，数据量大于阈值，采用堆排序。
    |-- __final_insertion_sort # 插入排序整个排序区域。

2.3.2. 排序源码

排序源码：内省排序 + 插入排序。

/* /usr/include/c++/9/bits/stl_algo.h */

template<typename _RandomAccessIterator, typename _Compare>
inline void
sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
    _Compare __comp) {
    ...
    std::__sort(__first, __last, __gnu_cxx::__ops::__iter_comp_iter(__comp));
}

template<typename _RandomAccessIterator, typename _Compare>
inline void
__sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
    _Compare __comp) {
    if (__first != __last) {
        /* 内省排序：
         * 快速排序递归一定深度，如果对应区域内数据量大于阈值，对应区域内数据采用堆排序。 
         * std::__lg() 计算递归深度限制。*/
        std::__introsort_loop(__first, __last,
            std::__lg(__last - __first) * 2,  __comp);
        /* 插入排序。 */
        std::__final_insertion_sort(__first, __last, __comp);
    }
}

2.3.2.1. 内省排序

/* /usr/include/c++/9/bits/stl_algo.h */

template<typename _RandomAccessIterator, typename _Size, typename _Compare>
void
__introsort_loop(_RandomAccessIterator __first,
            _RandomAccessIterator __last,
            _Size __depth_limit, _Compare __comp) {
    while (__last - __first > int(_S_threshold)) {
        if (__depth_limit == 0) {
            /* 子区域采用堆排序。 */
            std::__partial_sort(__first, __last, __last, __comp);
            return;
        }
        --__depth_limit;
        /* 递归排序，并返回排序区域被分成两个区域后，区域的分界位置 __cut。 */
        _RandomAccessIterator __cut =
        std::__unguarded_partition_pivot(__first, __last, __comp);
        /* 快速排序（递归）。*/
        std::__introsort_loop(__cut, __last, __depth_limit, __comp);
        __last = __cut;
    }
}

/// This is a helper function...
template<typename _RandomAccessIterator, typename _Compare>
inline _RandomAccessIterator
__unguarded_partition_pivot(_RandomAccessIterator __first,
            _RandomAccessIterator __last, _Compare __comp) {
    /* 数据区域中间位置。 */
    _RandomAccessIterator __mid = __first + (__last - __first) / 2;
    /* 比较三个值：第一个位置 ，最后一个位置，中间位置这三个值。
     * 哪个位置上的数据处于中间的（a < b < c 取 b）作为快速排序的哨兵。
     * 那么将哨兵数据与第一个位置数据置换。 */
    std::__move_median_to_first(__first, __first + 1, __mid, __last - 1, __comp);
    /* 第一个位置上的数据是哨兵，那么从 [__first + 1, __last) 这个区间的数据，
     * 根据哨兵的值，将这个区域的数据分成左右两部分，
     * 例如：小于哨兵的数据放在区域左边，大于哨兵的数据放在区域右边。*/
    return std::__unguarded_partition(__first + 1, __last, __first, __comp);
}

/* 三个数取中值，放在 __result 位置。*/
template<typename _Iterator, typename _Compare>
void __move_median_to_first(_Iterator __result,_Iterator __a, _Iterator __b,
            _Iterator __c, _Compare __comp) {
    if (__comp(__a, __b)) {
        if (__comp(__b, __c))
            std::iter_swap(__result, __b);
        else if (__comp(__a, __c))
            std::iter_swap(__result, __c);
        else
            std::iter_swap(__result, __a);
    }
    else if (__comp(__a, __c))
        std::iter_swap(__result, __a);
    else if (__comp(__b, __c))
        std::iter_swap(__result, __c);
    else
        std::iter_swap(__result, __b);
}

/* 根据哨兵，将数据区域分成两部分，并返回区域分界位置。 */
template<typename _RandomAccessIterator, typename _Compare>
_RandomAccessIterator
__unguarded_partition(_RandomAccessIterator __first,
            _RandomAccessIterator __last,
            _RandomAccessIterator __pivot, _Compare __comp) {
    while (true) {
        while (__comp(__first, __pivot))
        ++__first;
        --__last;
        while (__comp(__pivot, __last))
        --__last;
        if (!(__first < __last))
        return __first;
        std::iter_swap(__first, __last);
        ++__first;
    }
}

2.3.2.2. 插入排序

源码分析。

/* /usr/include/c++/9/bits/stl_algo.h */

template <typename _RandomAccessIterator, typename _Compare>
void
__final_insertion_sort(_RandomAccessIterator __first,
                        _RandomAccessIterator __last, _Compare __comp) {
    if (__last - __first > int(_S_threshold)) {
        std::__insertion_sort(__first, __first + int(_S_threshold), __comp);
        std::__unguarded_insertion_sort(__first + int(_S_threshold), __last,  __comp);
    } else
        std::__insertion_sort(__first, __last, __comp);
}

/// This is a helper function for the sort routine.
template <typename _RandomAccessIterator, typename _Compare>
void
__insertion_sort(_RandomAccessIterator __first,
                    _RandomAccessIterator __last, _Compare __comp) {
    if (__first == __last) return;

    for (_RandomAccessIterator __i = __first + 1; __i != __last; ++__i) {
        /* 如果当前数据比第一个数据还要小（如果是从小到大排序），
         * [__first, __i) 区域数据向右移动一个位置，__i 数据放在首位。 */
        if (__comp(__i, __first)) {
            typename iterator_traits<_RandomAccessIterator>::value_type
                __val = _GLIBCXX_MOVE(*__i);
            _GLIBCXX_MOVE_BACKWARD3(__first, __i, __i + 1);
            *__first = _GLIBCXX_MOVE(__val);
        } else
            /* __i 位置上的数据作为要插入的数据，
             * 从右到左（__i 位置开始）逐个数据进行比较排序，直到不满足条件再停下来。 */
            std::__unguarded_linear_insert(__i,
                __gnu_cxx::__ops::__val_comp_iter(__comp));
    }
}

template <typename _RandomAccessIterator, typename _Compare>
void
__unguarded_linear_insert(_RandomAccessIterator __last, _Compare __comp) {
    typename iterator_traits<_RandomAccessIterator>::value_type
        __val = _GLIBCXX_MOVE(*__last);
    _RandomAccessIterator __next = __last;
    --__next;
    while (__comp(__val, __next)) {
        *__last = _GLIBCXX_MOVE(*__next);
        __last = __next;
        --__next;
    }
    *__last = _GLIBCXX_MOVE(__val);
}

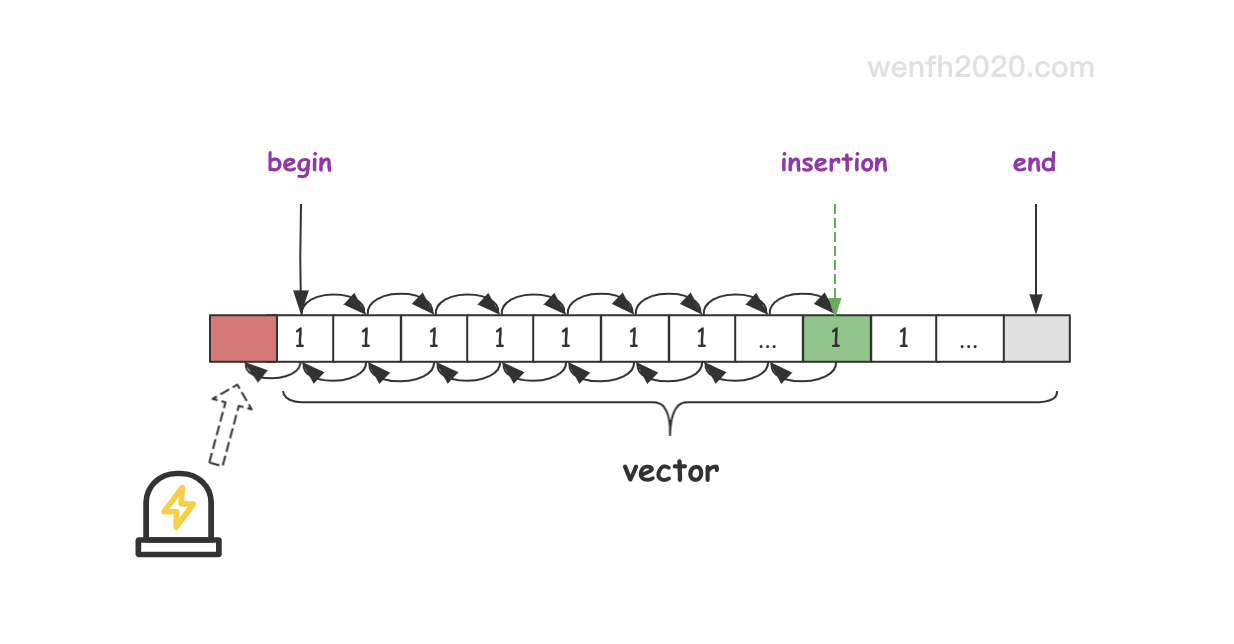
注意，因为 __unguarded_linear_insert 内部 while 循环没有作边界检查，所以 __comp 函数两个参数的比较必须是 v1 > v2 或者 v1 < v2，不能 v1 >= v2 或者 v1 <= v2 这样的，否则程序可能会因为内存越界崩溃（参考下面错误示例）。

/* g++ main.cpp -o test && ./test */
#include <algorithm>
#include <iostream>
#include <vector>

int main() {
    std::vector<int> nums;
    for (int i = 0; i < 100; i++) {
        nums.push_back(1);
    }
    std::sort(nums.begin(), nums.end(), [](int v1, int v2) {
        return v1 <= v2;
    });
    return 0;
}

3. 小结

std::sort 采用的是分治思维，先采用快速排序，将整个区域分成多个子区域，每个子区域内部根据数据量采用不同算法。
分治后，各个子区域局部有序后再通过整个区域进行排序。

[stl 源码分析] std::sort

1. 概述

1.1. 算法优缺点

1.2. 算法结合

2. 源码

2.1. 测试

2.2. 调试

2.3. stl 源码分析

2.3.1. 函数调用关系

2.3.2. 排序源码

2.3.2.1. 内省排序

2.3.2.2. 插入排序

3. 小结

4. 参考