[redis 源码走读] 跳跃表(skiplist)

张铁蕾的博客将 skiplist 原理和算法复杂度描述得很清楚，具体可以参考。我分享一下自己对部分源码的阅读情况和思考。

1. 数据结构
2. 思路
3. 接口
- 3.1. 插入结点
- 3.2. 流程描述
4. 调试
5. 参考

1. 数据结构

跳跃表是一个有序的双向链表。理解 zskiplistNode 的 zskiplistLevel 是理解zskiplist工作流程的关键。

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span; // 当前结点与 forward 指向的结点距离（跨越多少个结点），排名中应用。
    } level[]; // 层，可以理解结点的垂直纬度。
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

2. 思路

跳跃表是链表，链表查找时间复杂度是 O(n)，一般情况下，顺序查找比较慢。那比较取巧的，因为数据是顺序的，我们可以跳着找。例如下面 1 - 13 的数字，我们要找 9 这个数字。跳着找的流程是这样的:

跳跃查找

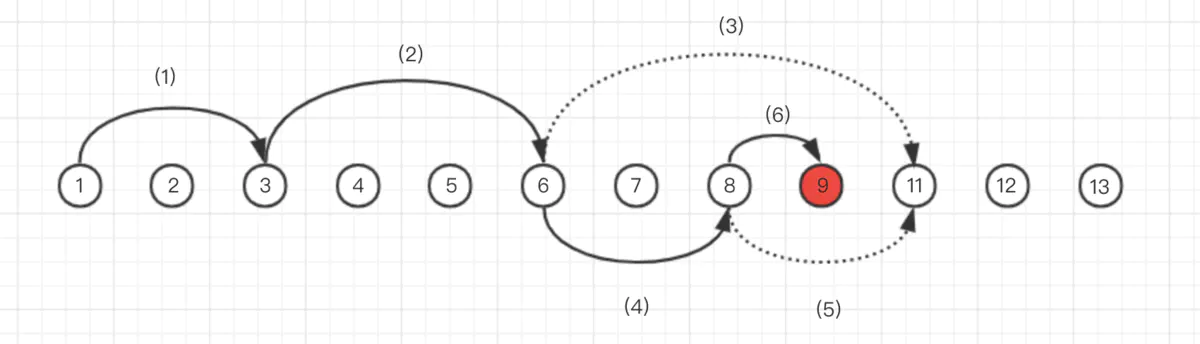
在第三步发现 11 比 9 大，就尝试跳更小的间距寻找合适的数据。同样的以此类推直到找到我们需要的数据。这样比我们顺序找要快很多。我们可以拆分一下上图的查找流程。每次查找不到时，就重新定向查找。每次重新定向查找被看作一个层。

拆分层次

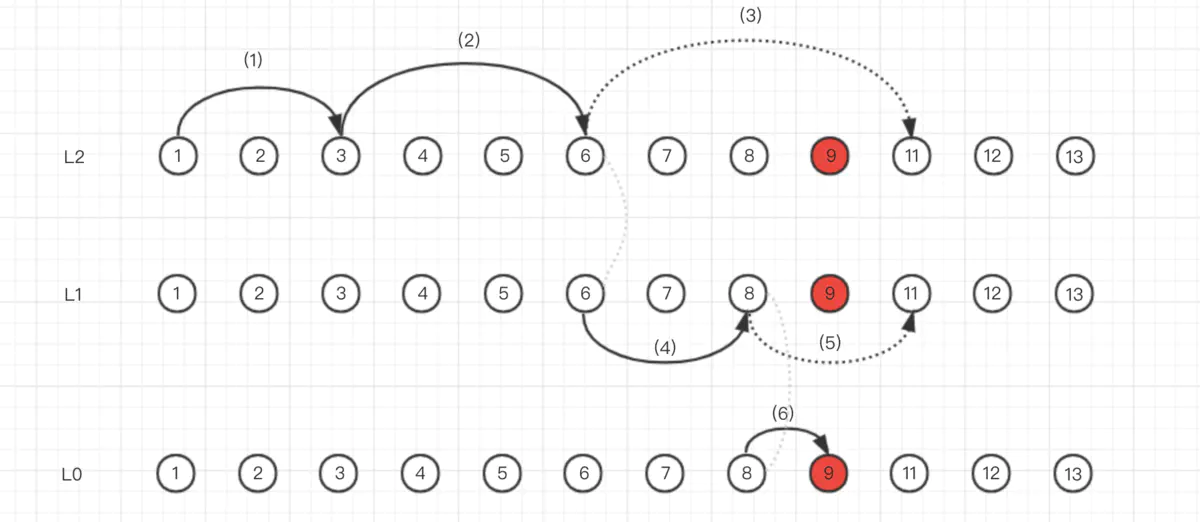
链表的层次，类似一个二维空间。每个结点有若干层，每一层将结点连接在一起建立关系，查找时 level 从最高层自上而下，结点从左到右。

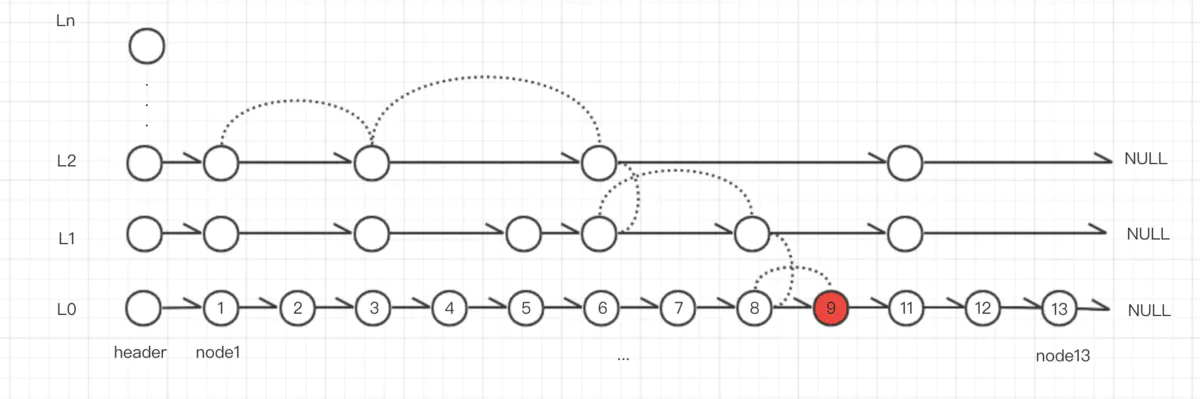
随机层 level，层数越高，概率越小。

#define ZSKIPLIST_MAXLEVEL 64 /* Should be enough for 2^64 elements */
#define ZSKIPLIST_P 0.25      /* Skiplist P = 1/4 */

int zslRandomLevel(void) {
    int level = 1;
    // 每增加一层概率是 ZSKIPLIST_P，所以层数越高，概率越小。
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    // 最高层数 ZSKIPLIST_MAXLEVEL
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

3. 接口

3.1. 插入结点

sorted set 功能实现，跳跃表结合 dict 使用。

// 跳跃表并不是单独使用的，在 sorted set 中，结合 dict 使用。
typedef struct zset {
    dict *dict; // 保存 ele 数据作为 key
    zskiplist *zsl; // 跳跃表存储 ele
} zset;

int zsetAdd(robj *zobj, double score, sds ele, int *flags, double *newscore) {
    ...
    znode = zslInsert(zs->zsl,score,ele);
    serverAssert(dictAdd(zs->dict,ele,&znode->score) == DICT_OK);
    ...
}

跳跃表插入结点。

/* Insert a new node in the skiplist. Assumes the element does not already
 * exist (up to the caller to enforce that). The skiplist takes ownership
 * of the passed SDS string 'ele'. */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    // update 保存每层遍历到满足条件的最后一个结点。
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;

    // rank 排名保存 span 结点间距。
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    // 二维空间，level自上而下遍历，结点从头到尾遍历，找到合适的插入结点位置。
    serverAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        // 下层保存上层的步距。
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            // 结点距离数目。
            rank[i] += x->level[i].span;
            // 遍历下一个结点。
            x = x->level[i].forward;
        }

        // 保存 i 层满足条件的最后一个结点。
        update[i] = x;
    }

    /* we assume the element is not already inside, since we allow duplicated
     * scores, reinserting the same element should never happen since the
     * caller of zslInsert() should test in the hash table if the element is
     * already inside or not. */
    // 随机层数
    level = zslRandomLevel();
    if (level > zsl->level) {
        // 初始化新增加的层，指向头结点，步距是列表的长度（结点个数）。
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            // 新增的 level 上是有指向结点指针的。
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }

    // 创建新的结点保存数据。
    x = zslCreateNode(level,score,ele);

    // 插入结点到列表
    for (i = 0; i < level; i++) {
        // level 自下而上与同层的插入位置前后结点建立联系。
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        // span：在同一个层级，当前结点到下一个结点的距离。
        // rank[0] - rank[i] 是插入位置，到 i 层所在结点的，结点距离。
        // update[i]->level[i].span 是插入位置到下一个结点到距离。
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 在 update[i] 后面添加了一个结点，span + 1
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    // 处理双向结点的前后结点连接关系。
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

3.2. 流程描述

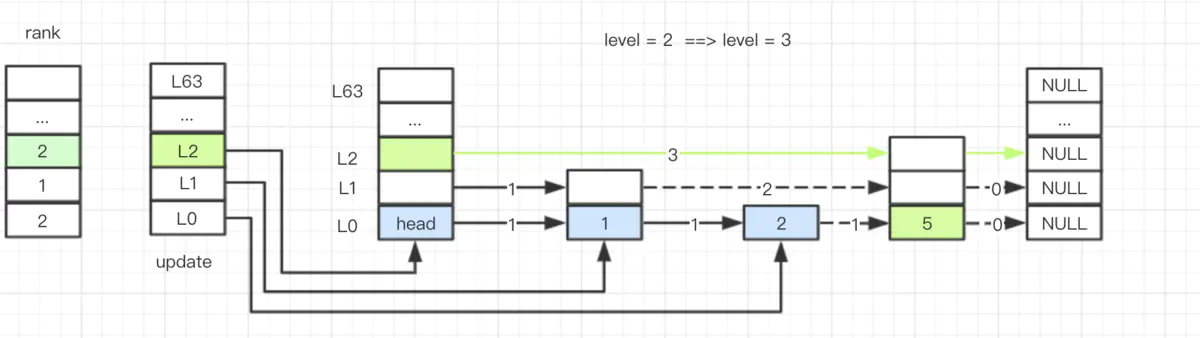
当 level 为 2 的链表，插入 level 为 3 的结点 5。（这里忽略了 ele 和 score 的处理）

插入数据的流程其实比不复杂，对于源码的理解，最好结合图表，这样大脑思考比较便捷。

插入前

插入前

插入后

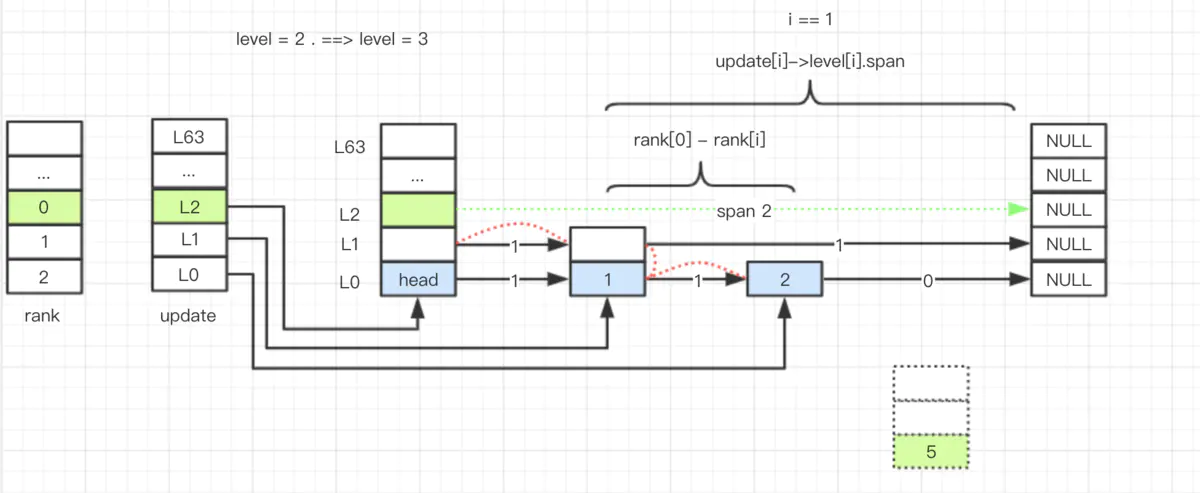
插入后

4. 调试

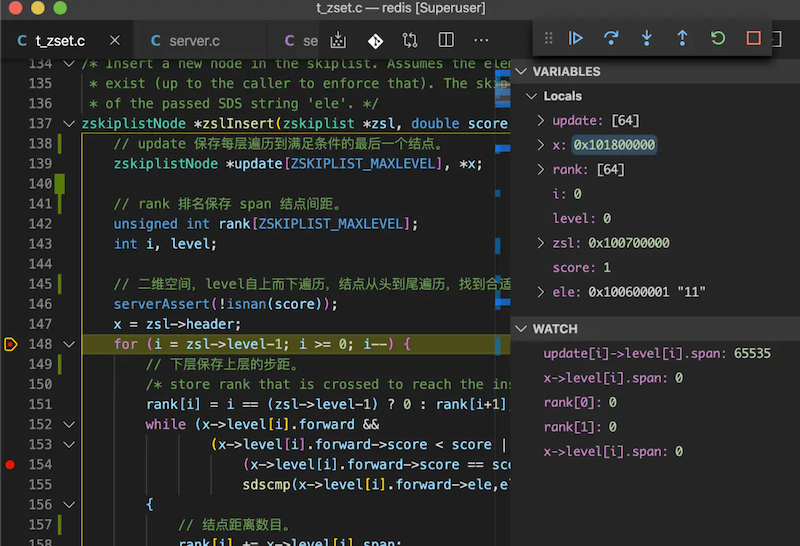
可以修改 redis 源码，跟踪一下工作流程。

调试方法可以参考我的帖子：用 gdb 调试 redis

server.c

int main(int argc, char **argv) {
    struct timeval tv;
    int j;

    zsetTest();
    return -1;
    ...
}

t_zset.c

void zsetTest() {
    sds ele;
    double score;
    zskiplist *zsl;
    zskiplistNode * node;

    score = 1;
    ele = sdsfromlonglong(11);

    zsl = zslCreate();
    node = zslInsert(zsl, score, ele);

    score = 2;
    ele = sdsfromlonglong(22);
    node = zslInsert(zsl, score, ele);
    zslFree(zsl);
}