[算法导论] 堆排序

学习《算法导论》堆排序算法，做了一些笔记。测试源码在 (github)

1. 堆
2. 堆排序过程
3. 优先队列
4. 参考

1. 堆

堆可以看成一个近似的完全二叉树，除了底层外，该树是完全充满的，而且是从左到右填充。

完全二叉树适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。

最大堆中，是指除了根结点外（根结点没有 parent），所有结点的 i 都应该满足： $A[PARENT(i)] \ge A[i]$

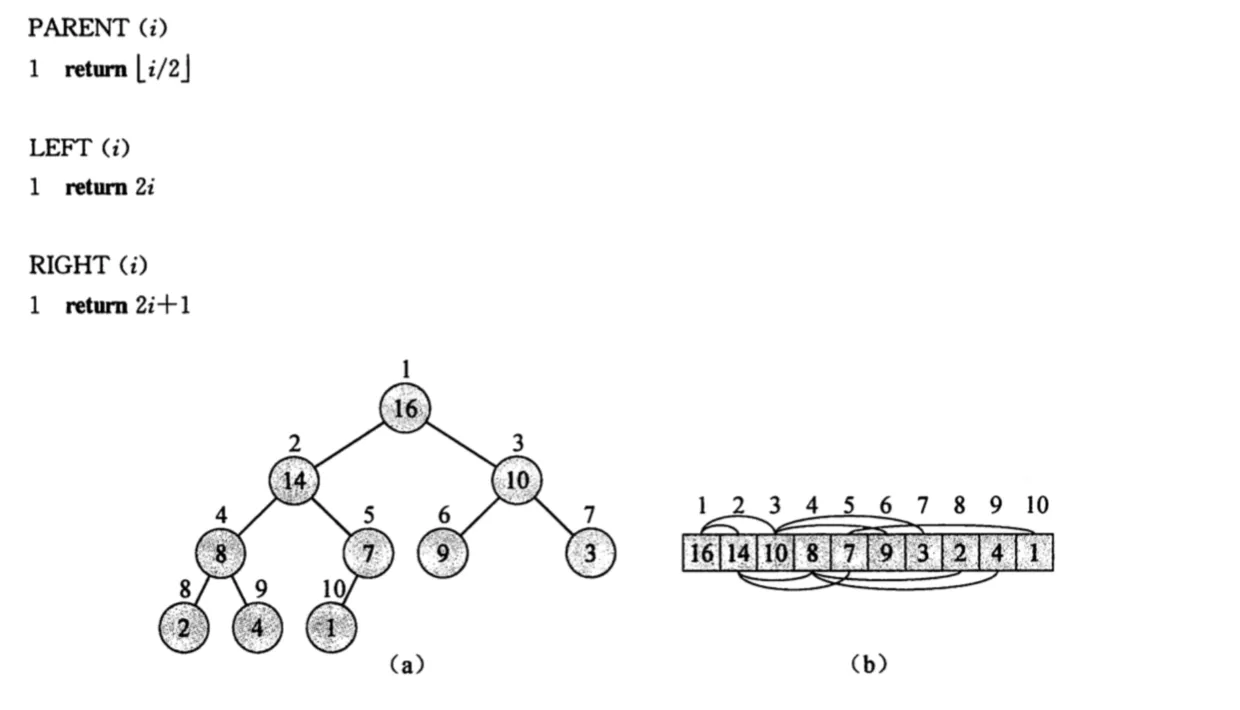
堆被看作是一个完全二叉树，那么该堆堆高度成正比 $O(lgn)$ ，我们会发现，堆结构上的一些基本操作的运行时间至多与树的高度成正比，即实际复杂度为 $O(lgn)$。

int parent(int i) { return i / 2; }
int left(int i) { return i << 1; }
int right(int i) { return (i << 1) + 1; }

2. 堆排序过程

堆化：将堆的 末端子 节点作调整，使得子节点永远 小于 父节点。
建堆：从无序数据数组中构造一个最大堆。
排序：将最大堆中的根节点（即最大值）与最后一个节点交换位置，并将最后一个节点从堆中移除。然后，对剩余的节点进行堆调整，使其重新满足最大堆的性质。重复这个过程，直到堆中只剩下一个节点。

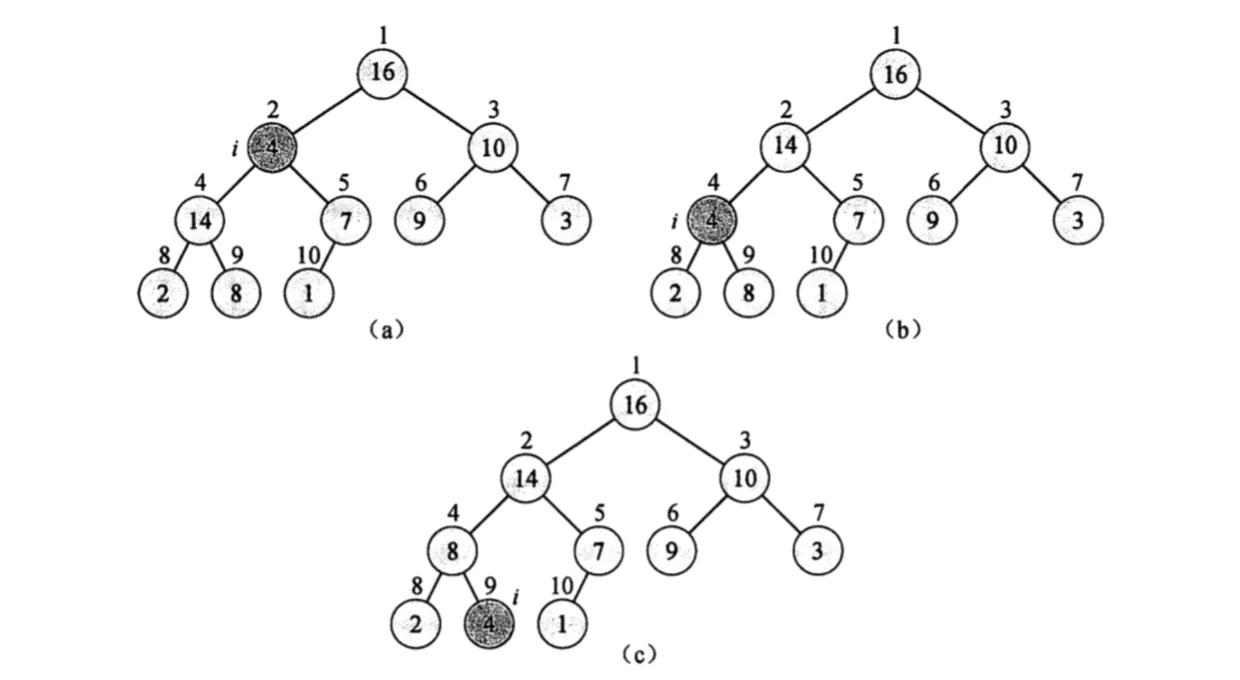
2.1. 堆化

堆化让数值大的结点往上浮，让小的结点逐渐下沉。

void max_heapify(int array[], int size, int i) {
    int largest = i;
    int l = left(i);
    int r = right(i);

    if (l <= size && array[l] > array[i]) {
        largest = l;
    }

    if (r <= size && array[r] > array[largest]) {
        largest = r;
    }

    if (largest != i) {
        swap(&array[largest], &array[i]);
        max_heapify(array, size, largest);
    }
}

2.2. 建堆

通过二叉树结点自底向上的方法，利用堆化过程，把一个大小为 n = A.length 的数组 A = [1…n] 转换为最大堆。建堆的时间复杂度为 $O(n)$。

void build_max_heap(int array[], int len) {
    for (int i = (len / 2); i >= 1; i--) {
        max_heapify(array, len, i);
    }
}

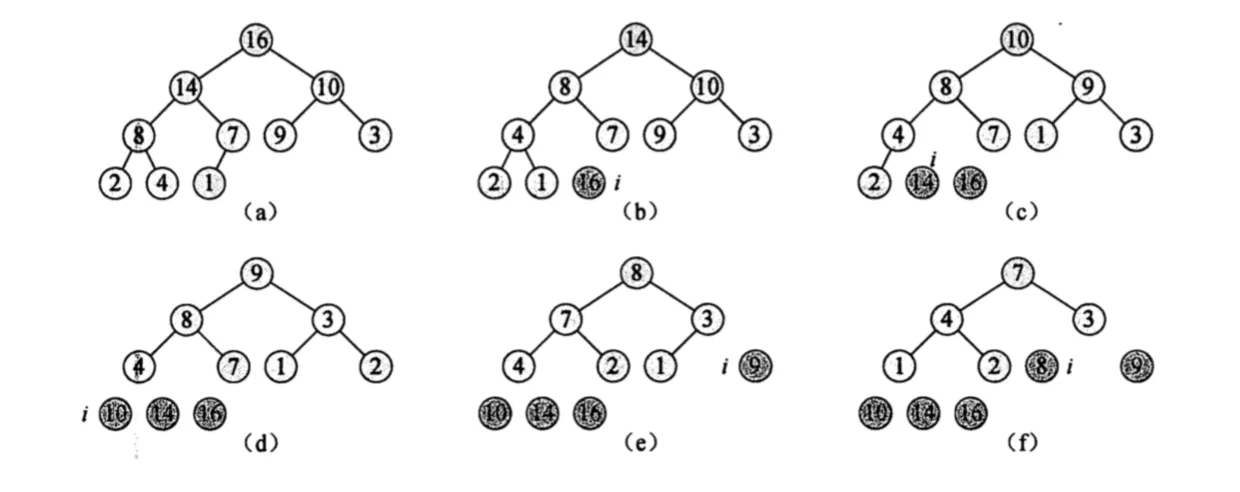
2.3. 排序

建堆会将数组 A[1…n] 建成最大堆，最大堆元素在根结点 A[1]，去掉 A[1] 后，A[1] 的左右孩子结点仍然是最大堆。
如果把 A[n] 替换 A[1]，破坏了最大堆性质，将重新对 A[1…n-1] 数组进行堆化，使其变成最大堆。
如此递归重复以上步骤。

void heap_sort::heap_sort() {
    if (m_data_size <= 1) {
        return;
    }

    // 建堆处理后，父结点 > 子结点
    build_max_heap(m_array, m_data_size);
    // 建堆后，堆顶结点（根结点）是最大数值，把最大值放到数组最后。原数组最后一个结点置换到根结点。
    swap(&m_array[1], &m_array[m_data_size]);

    // 排除数组最后一个元素，再对剩余堆进行堆化，再把堆化的根结点放到数组最后。
    m_data_size--;

    // 从上到下（父节点到子树结点）
    while (m_data_size > 1) {
        max_heapify(m_array, m_data_size, 1);
        swap(&m_array[1], &m_array[m_data_size]);
        m_data_size--;
    }
}

3. 优先队列

在计算机系统的作业调度中，任务需要根据优先级进行执行。可以根据堆算法（最大堆），每个任务都赋予一个优先级数值，选出最高优先级（最大堆堆顶）作业任务执行。涉及任务处理，一般都有增删改查的操作。理解了建堆，堆化和排序的流程，队列的这些操作应该都比较好理解了。

3.1. HEAP-MAXINUM

获取堆顶元素，时间复杂度为 $O(1)$

bool heap_sort::heap_maxinum(int& n) {
    if (m_data_size <= 0) {
        return false;
    }
    if (!m_is_build_heap) {
        build_max_heap(m_array, m_data_size);
    }
    n = m_array[1];
    return true;
}

3.2. HEAP-EXTRACT-MAX

删除堆顶元素，时间复杂度为 $O(n)$。

bool heap_sort::heap_extract_max(int& n) {
    if (m_data_size <= 0) {
        return false;
    }

    if (!m_is_build_heap) {
        build_max_heap(m_array, m_data_size);
    }

    n = m_array[1];
    swap(&m_array[1], &m_array[m_data_size]);
    m_data_size--;
    max_heapify(m_array, m_data_size, 1);
    return true;
}

3.3. HEAP-INCREASE-KEY

增加堆指定元素（任务）的数值，HEAP-INCREASE-KEY 时间复杂度为 $O(lgn)$。

bool heap_sort::heap_increase_key(int i, int key) {
    if (i < 1 || m_data_size <= 0 || key < m_array[i]) {
        return false;
    }

    if (!m_is_build_heap) {
        build_max_heap(m_array, m_data_size);
    }

    // 这里跟 build_max_heap 道理一样，只是 build_max_heap
    // 是自底向上，heap_increase_key 是从 i 结点向上
    m_array[i] = key;
    while (parent(i) > 0 && m_array[parent(i)] < m_array[i]) {
        swap(m_array[parent(i)], m_array[i]);
        i = parent(i);
    }
    return true;
}

3.4. MAX-HEAP-INSERT

插入新元素到最大堆末位，也就是在最大堆上增加一个叶子，叶子自下而上与它的父结点比较替换。运行时间复杂度为 $O(lgn)$

bool heap_sort::max_heap_insert(int key) {
    if (m_data_size >= m_data_len) {
        return false;
    }

    if (!m_is_build_heap) {
        build_max_heap(m_array, m_data_size);
    }

    // 将结点放置数组末位，也就是在最大堆上增加一个叶子，叶子自下而上与它的父结点比较替换。
    m_data_size++;
    m_array[m_data_size] = key;

    // 这是 heap_increase_key 主逻辑的实现。
    int i = m_data_size;
    while (parent(i) > 0 && m_array[parent(i)] < m_array[i]) {
        swap(m_array[parent(i)], m_array[i]);
        i = parent(i);
    }

    return true;
}