[算法导论] 归并排序

学习《算法导论》2.3.1 分治法。测试源码在 (github)

1. 时间复杂度
2. 视图
3. 实现
4. 参考

1. 时间复杂度

归并排序采用了分治法的递归排序。分治法：分解子问题，解决子问题，合并子结果。

分解：分解待排序的 $n$ 个元素的序列各成 $\frac{n}{2}$ 个元素的子列。
解决：使用归并排序递归地排序两个子序列。
合并：合并两个已排序的子序列以产生已排序的答案。

因为排序数组会被 $\frac{n}{2}$ 拆开，归并排序时间复杂度稳定的 $nlgn$。

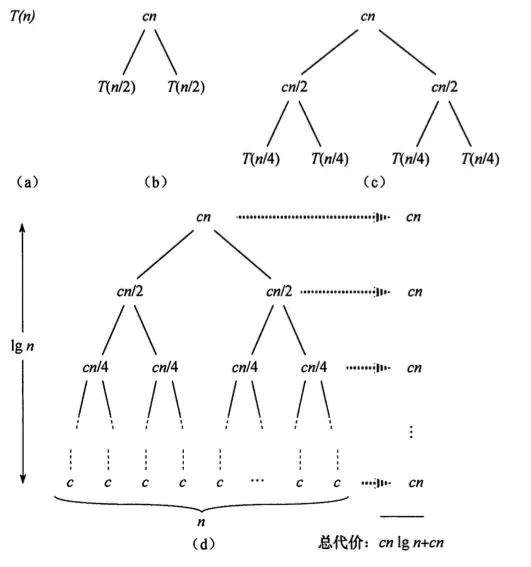
相对于其它的 $nlgn$ 排序，它需要额外的临时空间辅助，有一定的资源损耗。小数量级（百万级别）的排序，要比快速排序慢。但是大数量级数据（千万级别），因为归并排序树深最小，排序比快速排序快。

快速排序，最优算法复杂度，数组会被 $\frac{n}{2}$ 拆开。实际操作中数据很难达到最优。而归并一直都是通过 $\frac{n}{2}$ 进行拆分。

2. 视图

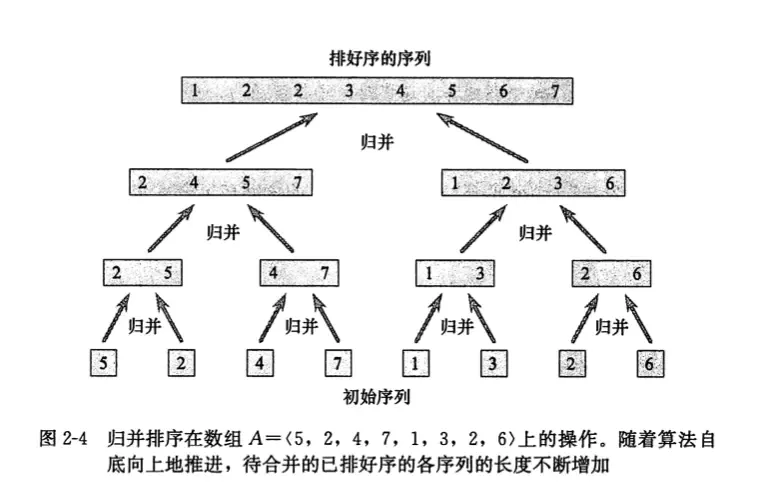
3. 实现

实际实现，通过一个辅助数组进行实现(源码)。

// g++ -g -O0 -std=c++11 test.cpp -o test && ./test
#include <iomanip>
#include <iostream>
#include <random>

void msort(int array[], int start, int mid, int end) {
    int k = 0;
    int low = start;
    int high = mid + 1;

    // 辅助的临时空间。
    int len = end - start + 1;
    int* temp_array = new int[len];

    // 合并两个有序数组到临时辅助空间上。
    while (low <= mid && high <= end) {
        if (array[low] < array[high]) {
            temp_array[k++] = array[low++];
        } else {
            temp_array[k++] = array[high++];
        }
    }

    // 区间没有拷贝完成的数据，继续拷贝到辅助的临时空间。
    while (high <= end) {
        temp_array[k++] = array[high++];
    }
    while (low <= mid) {
        temp_array[k++] = array[low++];
    }

    // 将临时空间的数据覆盖原空间对应数据。
    for (int i = 0; i < k; i++) {
        array[start + i] = temp_array[i];
    }

    delete [] temp_array;
}

void merge_sort(int array[], int start, int end) {
    if (start >= end) {
        return;
    }

    int mid = ((unsigned int)(start + end)) / 2;
    merge_sort(array, start, mid);
    merge_sort(array, mid + 1, end);
    msort(array, start, mid, end);
}

void print_datas(int array[], int size) {
    for (int i = 0; i < size; i++) {
        std::cout << std::setw(3) << array[i] << " ";
    }
    std::cout << std::endl;
}

bool is_sorted(int* array, int len) {
    if (array == nullptr || len < 2) {
        return true;
    }
    int max = array[0];
    for (int i = 1; i < len; i++) {
        if (max > array[i]) {
            return false;
        } else {
            max = array[i];
        }
    }
    return true;
}

void create_random_array(int** array, int* len, int max_value, int max_len) {
    std::random_device rd;
    *len = rd() % max_len;
    *array = new int[*len];

    for (int i = 0; i < *len; i++) {
        (*array)[i] = rd() % max_value;
    }
}

int main() {
    int len = 0;

    int max_len = 101;
    int max_value = 10000;
    int test_time = 100;

    for (int i = 0; i < test_time; i++) {
        len = 0;
        int* array = nullptr;
        create_random_array(&array, &len, max_value, max_len);

        if (array) {
            merge_sort(array, 0, len - 1);
            if (!is_sorted(array, len)) {
                std::cout << "failed!!!!!" << std::endl;
            }
            delete[] array;
        }
    }

    return 0;
}

4. 参考

快速排序、归并排序、堆排序三种算法性能比较
《算法导论》（第三版）