[算法导论] 快速排序

学习《算法导论》快速排序，需要重温数学知识，算法实现和推导是一个数学建模过程。测试源码在 (github)

1. 原理
2. 实现
3. 时间复杂度推导
4. 参考

1. 原理

对于包含 $n$ 个数的输入数组来说，快速排序是一种最坏情况时间复杂度为 $O(n^2)$ 的排序算法。

虽然最坏情况的时间复杂度很差，但是快排通常是实际排序应用中最好的选择，因为它平均性能非常好，它的期望实际复杂度是 $O(nlgn)$，而且 $O(nlgn)$ 中隐含的常数因子非常小，另外它还能够进行原址排序，甚至在虚存环境中也能很好地工作。

详细内容请参考《算法导论》第三版，第二部分，第七章：快速排序

2. 实现

根据数组哨兵的选择，有两种递归方式实现。

以数组末位数值为哨兵排序

int partition(int array[], int start, int end) {
    int low = start - 1;
    int high = low + 1;
    int key = array[end];

    for (; high < end; high++) {
        if (array[high] <= key) {
            low++;
            if (high > low) {
                int temp = array[low];
                array[low] = array[high];
                array[high] = temp;
            }
        }
    }

    // 如果是有序数组，会出现左边都是最小的情况，要置换 part_index 需要判断数据。
    int part_index = low + 1;
    if (array[part_index] > key) {
        int temp = array[part_index];
        array[part_index] = array[end];
        array[end] = temp;
    }

    return part_index;
}

void qsort_end(int array[], int start, int end) {
    if (start < 0 || end <=0 || start >= end) {
        return;
    }

    int part_index = partition(array, start, end);
    if (part_index >= 0) {
        qsort_end(array, start, part_index - 1);
        qsort_end(array, part_index + 1, end);
    }
}

以数组中间数值为哨兵排序

void qsort_mid(int array[], int start, int end) {
    if (start >= end) {
        return;
    }

    int high = end;
    int low = start;
    int key = array[(unsigned int)(start + end) / 2];

    while (low < high) {
        // 左边向右查找比 key 大的
        while (array[low] < key && low < end) {
            low++;
        }

        // 右边向左查找比 key 小的
        while (array[high] > key && high > start) {
            high--;
        }

        if (low <= high) {
            int temp = array[low];
            array[low] = array[high];
            array[high] = temp;
            low++;
            high--;
        }
    }

    qsort_mid(array, start, high);
    qsort_mid(array, low, end);
}

3. 时间复杂度推导

最优情况下的时间复杂度

快速排序涉及到递归调用，递归算法的时间复杂度公式： $T[n]=aT[\frac{n}{b}] + f(n)$ 数组共有 $n$ 个数值，最优的情况是每次取到的元素（哨兵）刚好平分整个数组。此时的时间复杂度公式为：$T(n)= 2T[\frac{n}{2}] + f(n)$

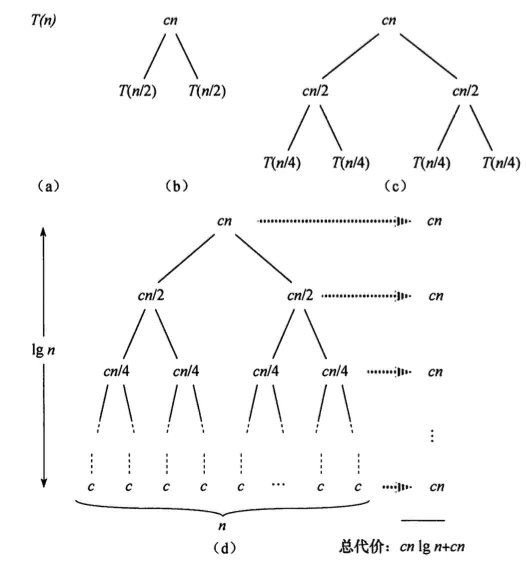
第一次递归： $T(n)= 2T[\frac{n}{2}] + f(n)$

第二次递归：令 $n = \frac{n}{2}$ , $T[\frac{n}{2}] = 2 {2T[\frac{n}{4}] + (\frac{n}{2})} + n = 2^2T[\frac{n}{(2^2)}] + 2n$

第三次递归：令 $n = \frac{n}{(2^2)}$ $T[\frac{n}{2^2}] = 2^2{2T[\frac{n}{2^3}] + \frac{n}{2^2}}+2n = 2^3T[\frac{n}{2^3}]+3n$

…

第 $m$次递归：令 $n = \frac{n}{2^{\left (m-1) \right.}}$ $T[\frac{n}{2^{\left(m-1)\right.}}] = 2^mT[1]+mn$

公式一直往下迭代，当最后数组不能再平分时，最后到$T[1]$，说明公式迭代完成（$T[1]$是常量）也就是：

$\frac{n}{2^{\left (m-1) \right.}} = 1$

$n = 2^{\left (m-1) \right.}$ ==> ( $n = 2^m$ ) ==> ( $m = log_2n$ )

当 $m = log_2n$ 时

$T[\frac{n}{2^{\left(m-1)\right.}}] = 2^mT[1]+mn = n + nlog_2n$

$n$ 为元素个数，当 $n \geq 2$ 时

$n + nlog_2n = n(1+log_2n) ==> nlog_2n ==> nlgn$

[算法导论] 快速排序

1. 原理

2. 实现

3. 时间复杂度推导

4. 参考